27. Gauss' Theorem
Let \(V\) be a nice solid region in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial V\), and let \(\vec F\) be a nice vector field on \(V\). Then \[ \iiint_V \vec\nabla\cdot\vec F\,dV =\iint_{\partial V} \vec F\cdot d\vec S \] The outer boundary must be oriented outward while any inner boundaries must be oriented inward. This means that all pieces of the boundary are oriented away from the solid.
d. Applications
4. Fluid Flow
Let \(\vec V\) be the velocity field of a fluid flowing in and out of a cylinder with a vertical axis. Then Gauss' Theorem says: \[ \iiint_C \vec\nabla\cdot\vec V\,dV =\iint\limits_\text{top, up} \vec V\cdot d\vec S +\iint\limits_\text{bot, down} \vec V\cdot d\vec S +\iint\limits_\text{sides, out} \vec V\cdot d\vec S \]
Assume the fluid is incompressible, i.e. \(\vec\nabla\cdot\vec V=0\). Then in the above equation, \(\displaystyle \iiint_C \vec\nabla\cdot\vec V\,dV=0\). In addition, we move the first integral to the left side of the equation and flip its orientation. Then Gauss' Theorem says: \[ \iint\limits_\text{top, down} \vec V\cdot d\vec S =\iint\limits_\text{bot, down} \vec V\cdot d\vec S +\iint\limits_\text{sides, out} \vec V\cdot d\vec S \]
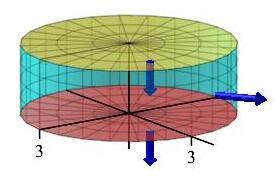
This says the flux of the fluid down through the top is equal to the flux down and out through the bottom and sides. As an example think of a leaky rain gauge. Since water is incompressible, the total water flowing into the top is equal the water flowing out the sides and bottom.
This example will compute both sides of this equation to verify they are equal.
Water is flowing with velocity \(\vec V=\langle xz+y^2,yz+x^2,-4-z^2\rangle\) through a cylinder with radius of \(3\) for \(0 \le z \le 2\). See the figure above. First check the water is incompressible. Then calculate the rate at which water flows into the top of the cylinder and the rate it flows out the sides and bottom of the cylinder.
We first check the water is incompressible: \[ \vec\nabla\cdot\vec V =z+z-2z=0 \]
Now we compute the flux of the water into the cylinder:
\(\displaystyle \iint\limits_\text{top, down} \vec V\cdot d\vec S\)
The top of the cylinder is a disk, parameterized as
\(\vec R(r,\theta)=(r\cos\theta,r\sin\theta,2)\). Thus the normal vector is:
\[
\vec N=\vec e_r\times\vec e_\theta
=\langle 0,0,r\rangle
\]
This normal vector is pointing upwards, but we want it oriented down, so we
reverse the direction: \(\vec N=\langle 0,0,-r\rangle\).
On the disk, the velocity is:
\[
\vec V=\langle xz+y^2,yz+x^2,-4-z^2\rangle
=\langle *,*,-8\rangle
\]
So the dot product with the normal is:
\[
\vec V\cdot\vec N
=\langle *,*,-8\rangle\cdot\langle 0,0,-r\rangle=8r
\]
Here, we write a \(*\) to indicate that we don't need to compute this
component, because it will not affect the dot product.
So the integral is
\[\begin{aligned}
\iint\limits_\text{top, down} \vec V\cdot d\vec S
&=\int_0^{2\pi}\int_0^3 \vec V\cdot\vec N\,dr\,d\theta
=\int_0^{2\pi}\int_0^3 8r\,dr\,d\theta \\
&=2\pi\left[\rule{0pt}{10pt}4r^2\right]_0^3=2\pi(36)
=72\pi
\end{aligned}\]
Now we compute the flux of the water out of the cylinder: \(\displaystyle \iint\limits_\text{bot, down} \vec V\cdot d\vec S +\iint\limits_\text{sides, out} \vec V\cdot d\vec S\) and compare with the answer above.
We now compute
\(\displaystyle \iint\limits_\text{bot, down} \vec V\cdot d\vec S\)
The bottom of the cylinder is a disk, parameterized as
\(\vec R(r,\theta)=(r\cos\theta,r\sin\theta,0)\). So
the normal vector for the bottom disk oriented down is
\(\vec N=\langle 0,0,-r\rangle\). On the disk
\[
\vec V=\langle xz+y^2,yz+x^2,-4-z^2\rangle=\langle *,*,-4\rangle
\]
So the dot product with the normal is
\[
\vec V\cdot\vec N=\langle *,*,-4\rangle\cdot\langle 0,0,-r\rangle=4r
\]
and the integral is
\[\begin{aligned}
\iint\limits_\text{bot, down} \vec V\cdot d\vec S
&=\int_0^{2\pi}\int_0^3 \vec V\cdot\vec N\,dr\,d\theta
=\int_0^{2\pi}\int_0^3 4r\,dr\,d\theta \\
&=2\pi\left[\rule{0pt}{10pt}2r^2\right]_0^3
=2\pi(18)
=36\pi
\end{aligned}\]
We finally compute
\(\displaystyle \iint\limits_\text{sides, out} \vec V\cdot d\vec S\)
The sides of the cylinder are parameterized as
\(\vec R(\theta,z)=(3\cos\theta,3\sin\theta,z)\). So the normal
vector for the sides of the cylinder is
\[\begin{aligned}
\vec N&=\vec e_z\times\vec e_\theta
=\begin{vmatrix}
\hat{\imath} & \hat{\jmath} & \hat{k} \\
0 & 0 & 1 \\
-3\sin\theta & 3\cos\theta & 0
\end{vmatrix} \\
&=\hat{\imath}(-3\cos\theta)-\hat{\jmath}( 3\sin\theta)+\hat{k}(0) \\
&=\langle -3\cos\theta,-3\sin\theta,0\rangle
\end{aligned}\]
This normal vector points inward, but we want it oriented outward, so we
reverse it:
\[
\vec N=\langle 3\cos\theta,3\sin\theta,0\rangle
\]
On the sides:
\[\begin{aligned}
\vec V&=\langle xz+y^2,yz+x^2,-4-z^2\rangle \\
&=\langle 3z\cos\theta+9\sin^2\theta,3z\sin\theta+9\cos^2\theta,-4-z^2\rangle
\end{aligned}\]
So the dot product with the normal is
\[\begin{aligned}
\vec V\cdot\vec N
&=9z\cos^2\theta+27\sin^2\theta\cos\theta+9z\sin^2\theta
+27\cos^2\theta\sin\theta+0 \\
&=9z+27(\sin^2\theta\cos\theta+\cos^2\theta\sin\theta)
\end{aligned}\]
and the integral is
\[\begin{aligned}
\iint\limits_\text{sides, out} \vec V\cdot d\vec S\,
&=\int_0^{2\pi}\int_0^2
[9z+27(\sin^2\theta\cos\theta+\cos^2\theta\sin\theta)]\,dz\,d\theta \\
&=\int_0^{2\pi} \left[\dfrac{9}{2}z^2+27z(\sin^2\theta\cos\theta
+\cos^2\theta\sin\theta)\right]_{z=0}^2\,d\theta \\
&=\int_0^{2\pi} [18+54(\sin^2\theta\cos\theta+\cos^2\theta\sin\theta)]\,d\theta \\
&=\left[18\theta+54\dfrac{\sin^3\theta}{3}
-54\dfrac{\cos^3\theta}{3}\right]_0^{2\pi}
=36\pi
\end{aligned}\]
We add the two together, \[ \iint\limits_\text{bot, down} \vec V\cdot d\vec S +\iint\limits_\text{sides, out} \vec V\cdot d\vec S =36\pi+36\pi=72\pi \] This result is the same as the first part of this example. Since the fluid is incompressible, the flux in equals the flux out.
Consider a fluid with velocity \[ \vec V=\langle x^3,y^3,-3(x^2+y^2)z\rangle \] flowing down through the disk, \(D\), given by \(x^2+y^2 \le 16\) with \(z=16\) and then through the paraboloid, \(P\), given by \(z=x^2+y^2\) for \(z \le 16\).
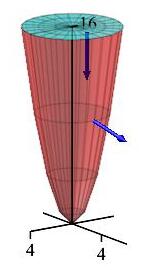
-
Find the flux through the disk, \(D\).
\(\displaystyle \iint\limits_\text{disk} \vec V\cdot d\vec S=6144\pi\)
The disk has radius \(4\). So it can be parameterized as \(\vec R(r,\theta)=(r\cos\theta,r\sin\theta,16)\) for \(r \le 4\). The normal vector is: \[ \vec N=\vec e_r\times\vec e_\theta =\langle 0,0,r\rangle \] which points upwards. So we reverse it: \(\vec N=\langle 0,0,-r\rangle\). On the disk, the velocity is: \[ \vec V=\langle x^3,y^3,-3(x^2+y^2)z\rangle =\langle *,*,-48r^2\rangle \] So the dot product with the normal is: \[ \vec V\cdot\vec N=48r^3 \] So the integral is \[\begin{aligned} \iint\limits_\text{disk} \vec V\cdot d\vec S &=\int_0^{2\pi}\int_0^4 \vec V\cdot\vec N\,dr\,d\theta =\int_0^{2\pi}\int_0^4 48r^3\,dr\,d\theta \\ &=2\pi\left[\rule{0pt}{10pt}12r^4\right]_0^4=24\pi(4^4) =6144\pi \end{aligned}\]
-
Find the flux through the paraboloid, \(P\).
Is the fluid incompressible?
\(\displaystyle \iint\limits_\text{paraboloid} \vec V\cdot d\vec S=6144\pi\)
We check to see if the fluid is incompressible: \[ \vec\nabla\cdot\vec V=3x^2+3y^2-3(x^2+y^2)=0 \] So the fluid is incompressible. Since the paraboloid and the disk have the same boundary curve, the flux through the paraboloid is the same as that through the disk: \[ \iint\limits_\text{paraboloid} \vec V\cdot d\vec S=6144\pi \]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum